Diamond
Theory
by Steven H. Cullinane |
Plato's
Diamond
|


Motto of
Plato's
Academy |
Abstract: Symmetry in Finite Geometry
Symmetry is often described as invariance under a group of
transformations. An unspoken assumption about symmetry in Euclidean 3-space is
that the transformations involved are continuous.
Diamond theory rejects this assumption, and in so doing reveals that
Euclidean symmetry may itself be invariant under rather interesting
groups of noncontinuous (and asymmetric) transformations. (These
might be called noncontinuous groups, as opposed to so-called
discontinuous (or discrete) symmetry groups. See Weyl's
Symmetry.)
For example, the affine group A on the 4-space over the 2-element field has
a natural noncontinuous and asymmetric but symmetry-preserving action on the
elements of a 4x4 array. (Details)
By embedding the 4x4 array in a 4x6 array, then embedding A in a supergroup
that acts in a natural way on the larger array, one can, as R. T. Curtis
discovered, construct the Mathieu group M24 -- which is, according
to J. H. Conway, the "most remarkable of all finite groups."
The proof that A preserves symmetry involves the following elementary, but
useful and apparently new, result: Every 4-coloring (i.e., every map into a
4-set) can be expressed as a sum of three 2-colorings. It is conceivable that
this result might have applications other than to diamond theory. (Details)
The proof that A preserves symmetry also yields some insight into
orthogonality of Latin squares, at least in the 4x4 case. In this case,
orthogonality turns out to be equivalent to skewness of lines in a finite
projective 3-space. (Details)
Diamond theory provides simple ways to visualize
- "the simplest non-trivial model for harmonic
analysis,"1 the Walsh functions,
- "the smallest perfect universe,"2 the finite
projective space PG(3,2),
- the "distinguished geometry," "remarkable geometric individual," and
"gem,"3 the finite projective plane PG(2,4),
- the "remarkable"4 outer automorphisms of
S6, and
- the structural equivalence of certain
- factorizations3 of graphs,
- parallelisms5 of partitions,
- spreads6 of lines, and
- sets of mutually orthogonal squares (i.e.,
n-orthogonal7 nxn matrices).
1. F. Schipp et al., Walsh
Series, 1990
2. Burkard Polster, website
3.
A. Beutelspacher in the American Mathematical Monthly, January 1986
4. P. J. Cameron and J. H. van Lint, Designs, Graphs,
Codes, and their Links, 1991
5. P. J. Cameron,
Parallelisms of Complete Designs, 1976
6. J. W. P.
Hirschfeld, Finite Projective Spaces of Three Dimensions, 1985
7. J. Denes and A. D. Keedwell, Latin Squares and their
Applications, 1974
As a bonus, extending the action of A to a 4x4x4 array yields a simple way
of generating the 1.3 trillion transformations natural to the 64 hexagrams of
the I Ching. (Details)

|
Mathematics Subject Classification (MSC2000) -
Primary:
20B25,
Finite automorphism groups of algebraic, geometric, or combinatorial
structures.
Secondary:
05B25, Finite geometries;
51E20,
Combinatorial structures in finite projective
spaces. |
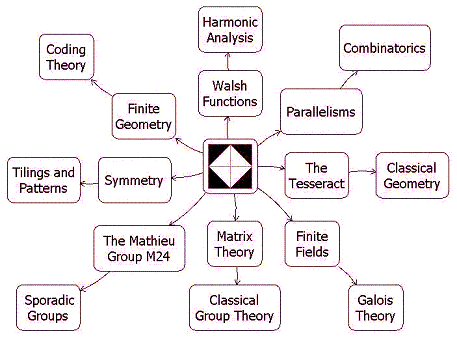
The following diagram is a rough sketch of how diamond theory is
related to some other fields of mathematics.
To Shirley
On Euclid's Elements:
"In view of...
admiration the Elements has consistently elicited over the years, and of
the prestigious role it concomitantly maintained until the mid-19th century as
scientific archetype, it is not surprising that we find in the history of
philosophy a concept of truth sustained by the example of the Elements,
whose influence in philosophy runs parallel to that of the Elements in
science. This concept I will call the 'Diamond Theory' of truth."
-- Richard
J. Trudeau in The Non-Euclidean Revolution, 1987
Introduction:
The image below shows the cover of a booklet I wrote
in 1976. The booklet details the implications of what I call the "diamond
theorem," after the diamond figure in Plato's Meno dialogue. This website, which
updates the booklet, is written for mathematicians and college students of
mathematics. For a less technical treatment of philosophical and literary
matters related to the diamond theorem, see Math16.com.

For some historical background to the diamond theorem, see
For material related to the diamond theorem, with a large
downloadable file of that material, see
Notes on Finite Geometry.
For some background on the philosophy of mathematics in general,
see
The Non-Euclidean
Revolution.
This 1987 book by Richard J. Trudeau, with a brief
introduction by H. S. M. Coxeter, traces in the recent history of geometry the
conflict between what Trudeau calls the "Diamond Theory of truth" and the
"Story Theory of truth" -- known to more traditional philosophers as
"realism" and "nominalism."
For more on Trudeau's version of diamond theory, see this site's
companion website, Math16.com.
For more on the story theory, consider the following quotation:
"The moral of my story is: Read Euclid and ask questions. Then
teach a course on Euclid and later developments arising out of these questions."
The quotation is from Robin Hartshorne, the author of Algebraic
Geometry, in "Teaching Geometry According to Euclid," Notices of the
American Mathematical Society, April 2000.
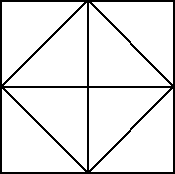
Diamond Theory
Plato tells how Socrates helped Meno's slave boy "remember" the
geometry of a diamond. Twenty-four centuries later, this geometry has a new
theorem.
The Diamond Theorem:Inscribe a white diamond in a black
square.
Split the resulting figure along its vertical and
horizontal midlines into four quadrants so that each quadrant is a
square divided by one of its diagonals into a black half and a white
half. Call the resulting figure D. |
|
|
Let G be the group of 24 transformations of D obtained by
randomly permuting (without rotating) the four quadrants of D. Let
S4 denote the symmetric group acting on four elements.
Then
(1) Every G-image of D has some ordinary or color-interchange
symmetry (see below),
(2) G is an affine group generated by S4 actions on
parts of D, and
(3) Results (1) and (2) generalize, through intermediate stages,
to symmetry invariance under a group of approximately 1.3 trillion
transformations generated by S4 actions on parts of a
4x4x4 cube. | |
The 2x2 case
In the 2x2 case, D is a one-diamond figure (top left, below) and G is
a group of 24 permutations generated by random permutations of the four
1x1 quadrants. Every G-image of D (as below) has some ordinary or
color-interchange symmetry. |
 |
Example of the
4x4 case
In the 4x4 case, D is a four-diamond figure (left,
below) and G is a group of 322,560 permutations generated by arbitrarily
mixing random permutations of rows and of columns with random permutations
of the four 2x2 quadrants. Every G-image of D (as at right, below) has
some ordinary or color-interchange symmetry. |

D |
Let e denote
transposition of the first two rows, f denote transposition of the
last two columns, g denote transposition of the top left and bottom
right quadrants, and h denote transposition of the middle two
columns. Then Defgh is as at right. Note that Defgh has
rotational color-interchange symmetry like that of the famed yin-yang
symbol. |

Defgh |
Remarks on the 4x4 case:
G is isomorphic to the affine group A on the linear 4-space
over GF(2). The 35 structures of the 840 = 35 x 24 G-images of D are
isomorphic to the 35 lines in the 3-dimensional projective space over
GF(2). Orthogonality of structures corresponds to skewness of lines. We
can define sums and products so that the G-images of D generate an ideal
(1024 patterns characterized by all horizontal or vertical "cuts" being
uninterrupted) of a ring of 4096 symmetric patterns. There is an infinite
family of such "diamond" rings, isomorphic to rings of matrices over
GF(4). For a movable JavaScript version of these 4x4 patterns, see The 16 Puzzle.
|
The statement of the theorem may be clarified by a research
announcement written in 1978 that illustrates the above 4x4 example in
reverse... Research
Announcement, 1978.
Illustrations of half-square patterns:
For an artist's rendering of some patterns generated as described
in the diamond theorem (and many not so generated), see the following new
(September 11, 2000) website: Tiling,
by Mike Lyon.
For more illustrations and a sketch of the proof, see the
following
Diamond Theory Research Notes
Hartshorne's principle: "Whenever one approaches a subject from
two different directions, there is bound to be an interesting theorem expressing
their relation." - Robin Hartshorne, AMS Notices, April 2000, p. 464.
- ( 1) Diamond
theory cover page
- From the author's 1976 booklet. See Math16.com for the meaning of the cover
illustration.
- ( 2) The
relativity problem in finite geometry
- "This is the relativity problem: to fix objectively a class of equivalent
coordinatizations and to ascertain the group of transformations S mediating
between them."
-- Hermann Weyl, The Classical Groups
For an
application to analysis, see Symmetry of Walsh Functions.
- ( 3) Orthogonality of
Latin squares viewed as skewness of lines
- Structural diagrams of 4x4 arrays play the role of lines in PG(3,2).
Orthogonality of arrays corresponds to skewness of lines.
- ( 3.1) Map systems
- The algebra underlying note (3): Every 4-coloring can be expressed, using
GF(4), as a linear combination of three 2-colorings. This elementary, but
apparently new, result may have applications other than to diamond theory.
- ( 4) Diamonds
and whirls
- Block designs of a different sort -- graphic figures on cubes. See also
the University of
Exeter page on the octahedral group O.
- ( 5) Affine
groups on small binary spaces
- Six ways to slice a cube, and the resulting affine groups.
For
details, see the author's 1984 paper Binary Coordinate Systems.
- ( 6) An
invariance of symmetry
- The diamond theorem on a 4x4x4 cube, and a sketch of the proof.
- ( 7) Generating the octad
generator
- The Miracle Octad Generator (MOG) of R. T. Curtis -- A correspondence
between the 35 partitions of an 8-set into two 4-sets and the 35 lines of
PG(3,2).
For more on the MOG, see, for instance, the preprint by Marston
Conder and John McKay, "Markings of the Golay Code" -- either the author's PostScript
version or the cached version.
Other details on the Miracle Octad Generator are given in the reference file
highlighted in yellow below.
- ( 8) The
2-subsets of a 6-set are the points of a PG(3,2)
- Beutelspacher's model of the 15 points of PG(3,2) compared with a 15-line
complex in PG(3,2).
- ( 9) Twenty-one projective
partitions
- The author's model of the 21-point projective plane PG(2,4).
For a
general method of constructing such models, see Modeling PG(2,4).
-
- (10) Inscapes
- A new combinatorial concept that illustrates symplectic polarities in
PG(3,2).
- (11) Inscapes
II
- The concept in note (10) is generalized.
- (12) Inscapes
III
- An excellent source of exercises related to note (12) is Introduction
to the Theory of Groups of Finite Order, by Robert D. Carmichael (1937),
reprinted by Dover Books, 1956. See especially
pp. 42-43, ex. 30 and 31;
p. 73, ex. 32;
p. 165, ex. 20;
p. 304, ex. 3;
pp. 320-321, ex.
7-12;
pp. 336-337, ex. 4-7, 9, 10;
p. 353, ex. 5;
p. 392, ex. 6,
part (3);
p. 437, ex. 14-17;
p. 439, ex. 11-12;
pp. 440-441, ex.
20, 21.
These exercises in Carmichael have a simplicity and clarity
lacking in many more recent works on finite mathematics.
See also
"Generalized Steiner Systems of Type 3-(v,{4,6},1)," by E. F. Assmus, Jr., and
J. E. Novillo Sardi, in Finite Geometries and Designs, edited by P. J.
Cameron, J. W. P. Hirschfeld, and D. R. Hughes, Cambridge University Press,
1981.
- (13) Inscapes
IV
- An outer automorphism that is literally outer.
- (14) Portrait
of O
- A table of the octahedral group O using the 24 patterns from the 2x2 case
of the diamond theorem.
- (15) Study of
O
- A different way of looking at the octahedral group, using cubes that
illustrate the 2x2x2 case of the diamond theorem.
- (16) Symmetry
invariance under M12
- A generalization of the two-color plane patterns, made up of all-black and
all-white squares, that underlie plane patterns, made up of two-color
diagonally-divided squares, of diamond theory.
Other research notes:
The above notes are directly related to the
diamond theorem. For 23 other research notes less directly related to, but
inspired (for the most part) by the theorem, see Miscellaneous Research Notes by S.
H. Cullinane.
Plato, Pythagoras, and the diamond figure:
Plato's
Diamond in the Meno
Plato as a precursor of Gerard Manley
Hopkins's "immortal diamond." An illustration shows the prototype of the figure
D discussed above.
Plato's Diamond
Revisited
Ivars Peterson's Nov. 27, 2000 column "Square of the
Hypotenuse" which discusses the diamond figure as used by Pythagoras (perhaps)
and Plato. Other references to the use of Plato's diamond in the proof of the
Pythagorean theorem:
Huxley --
"... and he proceeded to prove the theorem of Pythagoras --
not in Euclid's way, but by the simpler and more satisfying method which was, in
all probability, employed by Pythagoras himself....
'You see,' he said, 'it
seemed to me so beautiful....'
I nodded. 'Yes, it's very beautiful,' I said
-- 'it's very beautiful indeed.'"
-- Aldous Huxley, "Young Archimedes," in
Collected Short Stories, Harper, 1957, pp. 246 - 247
Heath --
Sir Thomas L. Heath, in his commentary on Euclid I.47, asks
how Pythagoreans discovered the Pythagorean theorem and the irrationality of the
diagonal of a unit square. His answer? Plato's diamond.
(See Heath, Sir
Thomas Little (1861-1940),
The thirteen books of Euclid's Elements
translated from the text of Heiberg with introduction and commentary. Three
volumes. University Press, Cambridge, 1908. Second edition: University Press,
Cambridge, 1925. Reprint: Dover Publ., New York, 1956. Reviewed: Isis 10
(1928),60-62.)
Other sites on the alleged "diamond" proof of Pythagoras --
Colorful diagrams at
Cut-the-Knot
Illustrated legend of
the diamond proof
Babylonian
version of the diamond proof
Keywords to help place the diamond theorem in the proper mathematical
context:
"We may say, roughly, that a mathematical idea is 'significant' if it can be
connected, in a natural and illuminating way, with a large complex of other
mathematical ideas."
- G. H. Hardy, A Mathematician's Apology (1940),
Cambridge University Press, reprinted 1969, page 89
affine geometry, affine planes, affine spaces, automorphisms, binary codes,
block designs, classical groups, codes, coding theory, collineations,
combinatorial, combinatorics, conjugacy classes, the Conwell correspondence,
correlations, Cullinane, R. T. Curtis, design theory, the diamond theorem,
diamond theory, duads, duality, error correcting codes, exceptional groups,
finite fields, finite geometry, finite groups, finite rings, Galois fields,
generalized quadrangles, generators, geometry, GF(2), GF(4), the (24,12) Golay
code, group actions, group theory, Hadamard matrices, hypercube, hyperplanes,
hyperspace, incidence structures, invariance, Karnaugh maps, Kirkman's
schoolgirls problem, Latin squares, Leech lattice, linear groups, linear spaces,
linear transformations, Mathieu groups, matrix theory, Meno, Miracle Octad
Generator, MOG, multiply transitive groups, octads, the octahedral group,
orthogonal arrays, outer automorphisms, parallelisms, partial geometries,
permutation groups, PG(3,2), Plato, Platonic, polarities, Polya-Burnside
theorem, projective geometry, projective planes, projective spaces,
projectivities, Reed-Muller codes, the relativity problem, Singer cycle, skew
lines, Socrates, sporadic simple groups, Steiner systems, Sylvester, symmetric,
symmetry, symplectic, synthemes, synthematic, tesseract, transvections, Walsh
functions, Witt designs
Search engine for use with the above keywords:
Other search engines:
Google
Directory of Mathematics Search Engines
Sites on combinatorics generally:
The Combinatorics Net
The Open Directory list of
combinatorics sites
U. of London Permutation Groups
Resources
U. of London Design
Resources on the Web
View notes from author's
personal journal
View list of
site updates.
An overview of titles in the above bibliography
as of
October 16, 2001:
The generalized Walsh functions
On the Walsh functions
Walsh series: an introduction to dyadic harmonic analysis
Review of the book Walsh Series and Transforms,
by Golubov, et al.
Walsh series and transforms
Transitive Erweiterungen endlicher Permutationsgruppen
Combinatorial theory
Permutation groups
Permutation groups and combinatorial structures
(London Math. Soc. lecture note series, 23)
Math 555: Theory of Finite Groups (PDF)
Mathieu groups
The Mathieu groups and designs (PDF)
Special linear groups generated by transvections
and embedded projective spaces (PDF)
Some groups generated by transvection subgroups
Another simple proof for the existence of the
small Witt design (PDF)
Walsh-Hadamard transforms: A literature survey
Shift register sequences (Revised edition)
Designs, graphs, codes and their links
Orthogonal arrays: Theory and applications
Group theory and generalizations
Projective and polar spaces
A permutation decoding of the Golay code
A new construction of binary Golay code (24,12,8) using
a group algebra over a finite field
Lecture notes for Math6406, Combinatorial Structures
Bibliography for projective geometry
Symmetries of cultures
Symmetries in physics: new reflections
Bibliography of works on symmetry (72 items)
Mathematics in art and architecture
Symmetry (Annotated bibliography)
Linear groups with an exposition of the Galois theory
Finite geometries and their automorphisms -- Classical groups
The geometry of the classical groups
As it might have been
Reconstructing simple group actions
Bibliography of mutually orthogonal Latin squares
A theorem in finite projective geometry and some applications
to number theory
Design theory, Volume I (Encyclopedia of mathematics and
Its applications , Vol. 69)
Design theory, Volume II (Encyclopedia of mathematics and
Its applications, Vol. 78)
CRC handbook of combinatorial designs
Mutually orthogonal Latin squares (MOLS)
Mutually orthogonal Latin squares: A brief survey of constructions
The CRC handbook of combinatorial designs (1995 website)
Markings of the Golay code
Visual mathematics
International Society for the Interdisciplinary Study of
Symmetry (ISIS-Symmetry)
The recent generalizations of colored symmetry
The mathematical theory of plane chromatic ornaments
Symmetry in science and art
Colored symmetry
Symmetry and ornament
Bibliography on symmetry
Walsh functions bibliography - Part I - Theory
Walsh functions bibliography - Part II - Applications
Lattices, linear codes, and invariants, Part II (PDF)
Lattices, linear codes, and invariants, Part I (PDF)
What is coding theory?
MA 3218 Coding Theory
Mathematical BBS (Excellent math portal at U. of Ferrara)
Walsh functions and their applications
A note on the Mathieu groups
Notes on digital coding
On the Mathieu group M24 and related topics
On representations of the Mathieu groups as collineation groups
Finite projective spaces of three dimensions
Projective geometries over finite fields
Latin squares and their applications
Finite permutation groups
A representation of the Mathieu group M24 as a collineation group
M24 and certain automorphic forms
The simple groups related to M24
A characterization of the alternating groups of degree 8 and 9
La geometrie des groupes classiques
The maximal subgroups of M24
Combinatorial configurations
Finite primitive permutation groups: A survey
Classical codes as ideals in group algebras
Niemeier lattices, Mathieu groups, and finite groups of
symplectic automorphisms of K9 surfaces
The subgroup structure of the finite classical groups
Codes from affine permutation groups
Decoding the ternary Golay code
Intersection of the Steiner systems of M24
Geometric interpretations of the 'natural' generators of
the Mathieu groups
Natural constructions of the Mathieu groups
Further elementary techniques using the Miracle Octad Generator
Orbit and coset analysis of the Golay and related codes
The geometry and cohomology of the Mathieu group M12
Geometry and symmetry
The sense of order
Geometric algebra
A characterization of designs related to the Witt system S(5,8,24)
The Mathieu groups
Decoding the Golay codes
On the construction of the Steiner system S(5,8,24)
t-designs from the large Mathieu groups
On the Mathieu groups M22, M23, M24, and the uniqueness of the
associated Steiner systems
A combinatorial construction of the small Mathieu designs and groups
Decoding the binary Golay code with miracle octad generators
The Steiner system S(5,6,12), the Mathieu group M12, and the "kitten"
Eight octads suffice
Der wunderschone Oktaden-Generator
Perfect codes and the Mathieu groups
Memoire sur la nombre de valeurs que peut acquirer une fonction....
Stereoscopic animated hypercube
The geometry of the Mathieu groups (PDF)
(Ch. 9 of Projective and polar spaces)
The subgroups of M24, or how to compute the table of marks
of a finite group
Finite geometry after Aschbacher's theorem: PGL(n,q)
from a Kleinian viewpoint
The Mathieu groups and their geometries (PDF)
Hidden angular momenta
Research Index
A history of finite simple groups
Constructing the isomorphism of A8 with GL(4,2) (PDF)
An introduction to Golay codes
Quotations related to combinatorics
Design Foundation (Chapter 11) (PDF)
Codes on graphs (PDF)
Program for making quilt-pattern designs
Coding theory and its application to the theory of sphere packing
The tetrahedral Golay code (PDF)
Tiling in PostScript and METAFONT -- Escher's Wink (PDF)
Singer cycles (An introduction to the applications of
geometry in cryptography)
Constructions of the Golay codes -- A survey (PDF)
Problems and lecture notes on the Polya-Burnside
enumeration theorem (PDF)
The Tiling Patterns of Sebastien Truchet....
Methode pour faire une infinité de desseins differents avec
des carreaux ....
Truchet & types: tiling systems and ornaments
The Art of Kenneth A. Huff
Coloriage de pavage dit
Tiling patterns derived from Truchet tile
The classical groups
PermGroup
The point-hyperplane design 2-(15, 7, 3)
Sur la fonction cinq fois transitive de 24 quantites....
Memoire sur l'etude des functions des plusieurs quantites.....
Permutation Groups
Uber Steinersche Systemen
Die 5-fach transitiven Gruppen von Mathieu
Permutation groups
The smallest perfect universe
Square of the hypotenuse
Meno
Dodecahedral faces of M12
Some thoughts on the number six
Generating the octad generator
Binary coordinate systems
Sphere packings, lattices, and groups
Twelve sporadic groups
Sporadic groups
Low rank representations and graphs for sporadic groups
Symmetry of the cube
The 3-space PG(3,2) and its group
21-6=15: A connection between two distinguished geometries
Modeling the 21-point plane with outer automorphisms of S6
Combinatorial mathematics
Cyclic projective planes
Projective geometry
Duality and symmetry: A matrix symmetrization problem
Generalized Steiner systems of type 3-(v, {4,6}, 1)
Introduction to the theory of groups of finite order
Tiling
The diamond theory of truth
The non-Euclidean revolution
Symmetry
From error-correcting codes through sphere packings to simple groups
The theory of error-correcting codes
The thirteen books of Euclid's elements, Volume I
Tilings and patterns
A mathematician's aesthetics
A new combinatorial approach to M24
Diamond theory
Symmetry invariance in a diamond ring (A.M.S. abstract 79T-A37)
Diamond theory
Three lectures on exceptional groups
Parallelisms of complete designs
"It is a good light, then, for those
That know the ultimate Plato,
Tranquillizing with this jewel
The torments of confusion."
-
Wallace Stevens,
Collected Poetry and Prose, page 21,
The
Library of America, 1997
Ordering
information for Wallace Stevens book
Home-page address of the author is http://www.m759.com.
URL address of this page is http://m759.freeservers.com.
Page last updated July 17, 2004; created June 21, 2000.
Copyright © 2001 by Steven H. Cullinane. All rights reserved.
For a large downloadable folder
containing this and many
related web pages,
see Notes on Finite
Geometry.



![]()
![]()
![]()
![]()


