(4x4 Case)
by Steven H. Cullinane
We regard
the four-diamond figure D at left as a 4x4 array of two-color
diagonally-divided square tiles.Let G be the group of 322,560 permutations of these 16 tiles generated by arbitrarily mixing random permutations of rows and of columns with random permutations of the four 2x2 quadrants.
THEOREM: Every G-image of D (as at right, below)
has some ordinary or color-interchange symmetry.
Example:
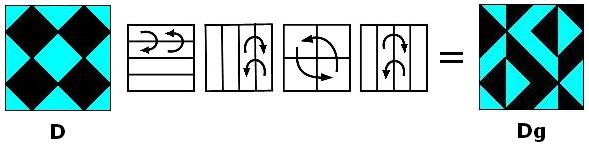
where g, a permutation in G, is a product of two disjoint
7-cycles. Note that Dg has rotational color-interchange symmetry
like that of the famed yin-yang symbol.
Remarks:
G is isomorphic to the affine
group A on the linear 4-space over GF(2). The 35 structures of the
840 = 35 x 24 G-images of D are
isomorphic to the 35 lines
in the 3-dimensional projective space over GF(2).
This can be seen by viewing the 35 structures as three-sets of line diagrams, based on the three partitions of the four-set of square two-color tiles into two two-sets, and indicating the locations of these two-sets of tiles within the 4x4 patterns. The lines of the line diagrams may be added in a binary fashion (i.e., 1+1=0). Each three-set of line diagrams sums to zero -- i.e., each diagram in a three-set is the binary sum of the other two diagrams in the set. Thus, the 35 three-sets of line diagrams correspond to the 35 three-point lines of the finite projective 3-space PG(3,2).
Among the 35 structures of the 840 4x4 arrays of tiles, orthogonality (in the sense of Latin-square orthogonality) corresponds to skewness of lines in the finite projective space PG(3,2). This was stated by the author in a 1978 note. (The note apparently had little effect. A quarter-century later, P. Govaerts, D. Jungnickel, L. Storme, and J. A. Thas wrote that skew (i.e., nonintersecting) lines in a projective space seem "at first sight not at all related" to orthogonal Latin squares.)
We can define sums and products so that the G-images of D generate an ideal (1024 patterns characterized by all horizontal or vertical "cuts" being uninterrupted) of a ring of 4096 symmetric patterns. There is an infinite family of such "diamond" rings, isomorphic to rings of matrices over GF(4).
The proof uses a decomposition technique for functions into a finite field that might be of more general use.
The underlying geometry of the 4x4 patterns is closely related to the Miracle Octad Generator (pdf) of R. T. Curtis-- used in the construction of the Steiner system S(5,8,24)-- and hence is also related to the Leech lattice, which, as Walter Feit has remarked, "is a blown up version of S(5,8,24)."
For a movable JavaScript version of these 4x4 patterns, see The Diamond 16 Puzzle.
This can be seen by viewing the 35 structures as three-sets of line diagrams, based on the three partitions of the four-set of square two-color tiles into two two-sets, and indicating the locations of these two-sets of tiles within the 4x4 patterns. The lines of the line diagrams may be added in a binary fashion (i.e., 1+1=0). Each three-set of line diagrams sums to zero -- i.e., each diagram in a three-set is the binary sum of the other two diagrams in the set. Thus, the 35 three-sets of line diagrams correspond to the 35 three-point lines of the finite projective 3-space PG(3,2).
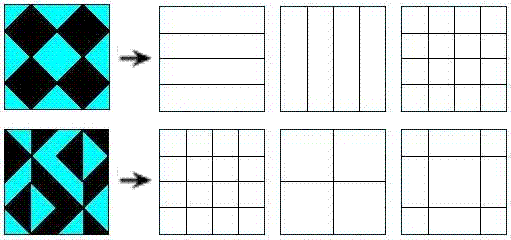
For example, here are the line diagrams
for the figures above:
for the figures above:
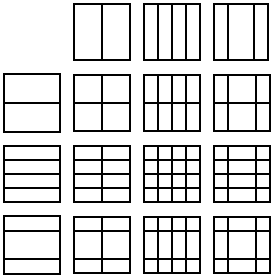
Shown below are the 15 possible line diagrams
resulting from row/column/quadrant permutations.
These 15 diagrams
may, as noted above, be regarded
as the 15 points of the projective
3-space PG(3,2).
The symmetry of the line diagrams accounts for the
symmetry of the two-color
patterns. (A proof shows that a 2nx2n two-color triangular
half-squares pattern with such line diagrams must have a 2x2 center with a
symmetry, and that this symmetry must be shared by the entire
pattern.)
Among the 35 structures of the 840 4x4 arrays of tiles, orthogonality (in the sense of Latin-square orthogonality) corresponds to skewness of lines in the finite projective space PG(3,2). This was stated by the author in a 1978 note. (The note apparently had little effect. A quarter-century later, P. Govaerts, D. Jungnickel, L. Storme, and J. A. Thas wrote that skew (i.e., nonintersecting) lines in a projective space seem "at first sight not at all related" to orthogonal Latin squares.)
We can define sums and products so that the G-images of D generate an ideal (1024 patterns characterized by all horizontal or vertical "cuts" being uninterrupted) of a ring of 4096 symmetric patterns. There is an infinite family of such "diamond" rings, isomorphic to rings of matrices over GF(4).
The proof uses a decomposition technique for functions into a finite field that might be of more general use.
The underlying geometry of the 4x4 patterns is closely related to the Miracle Octad Generator (pdf) of R. T. Curtis-- used in the construction of the Steiner system S(5,8,24)-- and hence is also related to the Leech lattice, which, as Walter Feit has remarked, "is a blown up version of S(5,8,24)."
For a movable JavaScript version of these 4x4 patterns, see The Diamond 16 Puzzle.